지도 학습과 비지도 학습
지도학습 (Supervised learning)
Tag를 가진 sample(x,t)로 구성된 학습 model 사용
•x는 특징 벡터이고 t는 x가 속한 부류
학습 모델
학습 모델은 매개변수 집합 Θ로 표현됨 (예, 그림 8-3에서 Θ는 분할 경계선을 표현)
모델 선택이 필요하면 추가적으로 검증 집합 사용
학습의 목표는 최적의 Θ 값을 찾는 것
•Θ 값이 얼마나 좋은지 측정하는 목적 함수 필요
학습 알고리즘의 원리
학습 집합을 사용하여 현재 Θ 값을 평가한 후, 개선하는 방향을 알아내 갱신
이런 과정을 수렴할 때까지 반복 error를 줄이는 방법으로 Θ 변경
일반화 능력
학습 과정에서 사용하지 않은 테스트 집합으로 학습이 완료된 분류기 성능을 평가
학습 집합과 테스트 집합에 대한 성능이 비슷하면 일반화 능력이 뛰어남
과적합(overfitting) 하면 일반화 능력이 떨어짐

비지도 학습(Unsupervised learning)
지도 학습에서 사용했던 (x,t) 중에 부류(class) 정보 t가 없는 상황의 학습
유사한 특징 벡터들을 끼리끼리 모으는 군집화(데이터를 유사한것끼리 묶는다) 수행 (K-means, SOM 신경망, 민시프트 등의 군집화 알고리즘)
군집에서 유용한 정보 추출 (데이터 마이닝, 빅데이터, 정보 검색 등의 많은 응용)
준지도 학습 //중요 x
부류 정보가 있는 샘플과 없는 샘플이 섞여 있는 상황의 학습
최근 중요성 부각
•아직 부류 정보를 부여하지 못한 샘플이 시시각각 인터넷에서 발생하기 때문
원리
•부류 정보가 있는 샘플로 학습한 후 부류 정보가 없는 샘플의 부류 정보를 추정
•추정된 정보로 반복 학습
신경망
신경망은 연결주의(connectionist) 계산 모형
방대하게 연결된 많은 뉴런(인간의 CPU)으로 구성된 뇌 구조를 모방한 계산 모형
1950년대 Rosenblatt의 퍼셉트론
1980년대 퍼셉트론을 확장한 다층 퍼셉트론(MLP)
일반화 능력이 뛰어나다. 지 알아서함ㅎ
퍼셉트론
1950년대에 나옴
퍼셉트론의 한계가 증명되어서 1970년대 AI의 winter라고한다.
입력은 특징 벡터 x=(x_1, x_2, …, x_d)
x를 두 개의 부류 ω1과 ω2 중의 하나로 분류하는 이진 분류기

입력층가 출력층이 있다.
w_1과 w_2로 분류하는 이진 분류기이다. // 1, -1
흰 노드는 전달 회색 노드는 합, 활성함수 계산 순차적 수행.
특징 벡터 : x, 가중치 벡터 : w, t(.) : 활성함수.
s = sum(x_i*w_i) y = t(s)

w*x^t --> (n x 1) * (1 x n)

신경망
일반적으로 입력층(input layer), 은닉(hidden)층, 출력(output)층으로 구성됨
- 은닉층: 결과가 바로 관찰되지는 않지만 중간 계산 과정에 포함되는 연결 부분
각 층은 일정한 개수의 neuron(신경세포)으로 구성됨

depth = 2 이것을 늘리는게 어려웠다. 3이상이 되면 deep learning이라고 한다.
요즘은 100개이상이 될정도로 신경망의 성능이 좋아졌다. 컴퓨터 성능의 향상으로 많이 좋아짐.
w를 찾아내는게 문제이다. --> learning
뉴런
뉴런은 퍼셉트론과 유사하지만 다른 형태의 활성화함수를 사용

뇌의 connect은 계속 바뀐다.
자주 사용되는 활성화 함수
활성화 함수는 비선형(nonlinear) 함수이며, 여러 개의 뉴런을 동시에 사용하면 다양한 함수 형태를 근사적으로 표현할 수 있음
Sigmoid
확률 표현에 적합
0 or 1 / -1 or 1

ReLU: Rectified linear unit
비선형!

신경망 학습
미리 준비된 입-출력 데이터(x_i, y_i, i = 1,...,N)를 이용하여 각 뉴런의 가중치(wj)를 결정하는 과정을 훈련(training)이라고 함
사례 : hand-written digit recognition

입력: 28x28 크기의 이진 영상. 784 크기의 벡터
출력: 0~9 까지의 10개의 클래스
은닉층: 15개의 뉴런으로 구성한다고 가정
학습시켜야 하는 계수 갯수:
784 x 15 + 15 x 10 = 11,910
Feed-forward computation
n현재의 계수들(wj)을 이용하여 각 은닉층 뉴런과 출력 뉴런의 값을 차례로 계산하는 과정

각 layer를 거칠 때 마다 convolution하는 것과 같은 연산을 한다.
Error (Loss) function
계수를 학습시키기 위해 각 입력 데이터로부터 생성된 출력값이 실제 클래스값과 얼마나 일치하는가에 대한 측정 수단이 필요
예: 숫자 인식의 경우 6에 해당하는 영상을 입력시켰을 때 원하는 출력값은

합이 1이 되긴 하지만 현재 실제 데이터 6인데 9라고 결론 내렸다.
초반에는 제대로된 결과를 못낸다. y-a으 차이가 많이 난다.
error는 차이를 제곱해서 다 더한 후 n으로 나누어서 연산.
Optimization 최적화
Loss 함수는 가중치 W의 함수이며, loss를 최소화하는 가중치들 W를 구하는 것이 문제임
앞 필기체 숫자 인식의 경우 11,910의 계수가 있으므로 L을 최소화하는 11,910개의 계수를 방정식으로 푸는 것은 불가능에 가까움
문제: 다음 그림에서와 같이 E(w1, w2,....,wm)을 최소화하는 가중치들 (w1,....,wm) 을 구함
Gradient descent (경사 하강법)
현재점에서의 gradient를 계산하여 그 방향으로 조금씩 이동하여 최저점에 도달하는 방식
최저점에서는 gradient가 0이므로 최저점에 도달하면 더 이상 움직이지 않음
Gradient descent를 사용하려면 각 가중치로 error 함수를 편미분한 식을 사용

윗 식에서 E는 error 함수, wt는 t 시점에서의 가중치, wt+1은 다음 시점에서의 가중치, h는 learning rate임. h의 크기에 따라 수렴속도가 달라짐
가중치는 매 데이터 샘플을 읽을 때마다 새로 갱신(update)하거나, 일정 개수의 sample(batch size)을 처리한 다음 갱신하기도 함
Epoch: 전체 입력 데이터로 가중치 갱신을 한 번 마치는 것. 일반적으로 신경망 학습과정은 수백번의 epoch을 반복하는 것으로 수행됨
Backpropagation
가중치를 update 할 때는 출력층을 먼저 update 하고 뒷단의 은닉층부터 앞 단으로 내려오면서 계산

Convolutional Neural Networks (CNN)
Fully-connected network
현 단계 뉴런 출력을 구하기 위해 이전 단계의 모든 뉴런을 입력으로 사용
Convolutional network
자기주변에 있는 것들만 가지고 convolution 연산을 통해 현 단계 뉴런의 출력을 계산

b : offset
Convolution
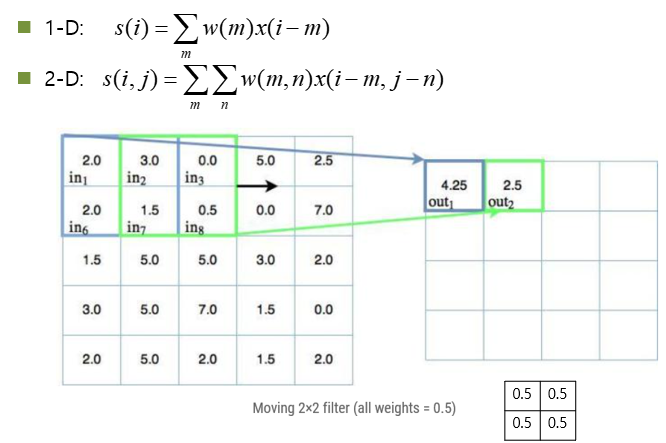
CNN의 특징과 장점
Sparse interaction
이전 계층에서 연결된 셀이 적다. (예: 5x5)
Parameter sharing
동일한 convolution mask를 전체 영상에서 적용. Full-connection 망의 경우 각 셀에서 서로 다른 weight wjk를 사용함
위의 두 가지 성질때문에 CNN에서는 parameter (weight) 숫자가 매우 줄어듦
CNN은 영상 인식 분야에서 많이 사용되고 있음
Convolution layer 구조
일정한 크기의 마스크(kernel)로convolution한 다음, 비선형 활성화 함수를 통해 출력을 얻음
- 활성화 함수로는 ReLU를 많이 사용
다중 마스크: 일반적으로 여러 장의 마스크를 이용하여 여러 출력 영상을 생성.
- 이 과정은 에지 검출시 수평, 수직 방향의 두 개의 마스크를 사용하는 것과 유사

Convolution layer를 다르게 표현한 사례
6개의 마스크(kernel)와 sigmoid 활성화 함수를 사용
-마스크가 내부로 모두 들어오는 점들에 대해서만 출력을 얻으면 출력 영상의 크기가 작아짐

Pooling
CNN에서는 일반적으로 convolution 연산층 다음에 pooling stage가 있음
-이전 계층의 2x2 (또는 다른 크기) 영역을 한 픽셀로 줄이는 과정
-2x2를 하나로 줄일 때 네 값 중 최대값(max)을 취하거나 평균값(avg)을 취할 수 있음

Pooling을 하는 이유
해상도를 낮추어(downsampling) 변수의 갯수를 줄임 //(데이터를 줄임)
영상 인식 과정에서 translation invariance를 도입하는 효과가 있음 //(보상이 되는 효과)
Stride
Convolution을 매 픽셀마다 수행하지 않고 일정 간격으로 건너 뛰면서 수행하는 것. Downsampling 효과를 얻을 수 있음
CNN 구조에서 stride를 사용하는 경우가 있음

Convolution 망 구성
망의 계층은 선형 convolution, 비선형 활성화 단계, pooling 등으로 구성

Convolution 출력단
CNN 출력단은 다시 fully-connected 형태의 출력단으로 구성

CNN 사례
두 단의 convolution-pooling 과정과 두 단의 fully connected layer, output layer로 구성. CONV 층은 ReLU를 포함한 것임

-f: filter size, s: stride, p: padding (상하좌우에 0을 채워 넣는 것. p=0 이면 padding을 하지 않았다는 의미임)
-Softmax: sigmoid 구조에 정규화과정을 추가하여 출력단의 합이 1이 되도록 만든 계층.
출력단으로 주로 사용함
Deep CNN으로 학습된 패턴 사례
Visualizing and Understanding Convolutional Networks, Zeiler & Fergus
상위 레이어로 진행될수록 보다 복잡한 패턴을 표현할 수 있음(학습할)
AlexNet
2012년에 발표된 대규모 CNN으로 약 120만 장의 영상으로 학습되어 1000개의 class를 구분할 수 있음
오차율: 15.4%
이후 보다 복잡하고 정확도가 높은 CNN 분류기가 발표되었으나 AlexNet은 비교적 단순한 구조를 가지고 있어서 계속 활용되고 있음: Matlab Deep Learning Toolbox에서도 사용할 수 있음
구조


AlexNet: Layer 1

AlexNet: Layer 1 Parameters

AlexNet: CNN Activation Function ReLU


'컴퓨터 비전' 카테고리의 다른 글
| 11장 3차원 비전 (0) | 2020.06.23 |
|---|---|
| 3장 에지 검출 - RANSAC (Random Sample Consensus) (0) | 2020.05.13 |
| 3장 에지 검출 - 허프변환(Hough Transform) (0) | 2020.05.13 |
| 3장 에지 검출 - 캐니 에지 (0) | 2020.05.12 |
| 3장 에지 검출 - 영교차 이론(Zero-crossing) (0) | 2020.05.12 |